想获得更多四川公务员备考咨询,欢迎关注官方微信号:htgwy01
行测备考技巧八 逻辑判断之必然性推理
逻辑判断是公务员考试中的必考题型,主要考查考生对逻辑知识的理解、分析、综合、判断、推理能力。从近几年四川公务员考试真题来看,逻辑判断题的题量在8-9题左右,考查内容一般分为必然性推理和可能性推理两个方面。其中,必然性推理是指从题目所给的前提条件必然能推出选项结论的命题。
许多初次接触逻辑判断题的考试,往往纠结于题目和选项的字面意思,发现怎么选都选不对,甚至会越想越糊涂,事实上,这是落入了做题的误区。逻辑题考查的并不是考生的阅读理解能力,而是抽象推理能力,因此,考生应把题目抽象成一定的逻辑关系,并按照逻辑推理的思路解题。下面,途途君就为大家总结一些必然性推理题中的命题形式和推理方法,供大家参考。
一、直言命题
(1)直言命题概念间的关系
直言命题,也称简单命题,是断定对象是否具有某种性质的单句。如“我们都是中国人”就是一个之言命题。其中,“我们”称为命题的主项;“中国人”称为命题的谓项;“都”称为命题的量项,“是”称为命题的联项。
判断一个命题的真假,主要看该命题是否与客观实际相符合,如果与客观实际相符合,则命题为真,如“小学生都是学生”;若与客观事实不相符,则命题为假,如“小孩子都是学生”。直言命题的真假是由主项和谓项在外延上所存在的关系决定的,具体如下表所示:
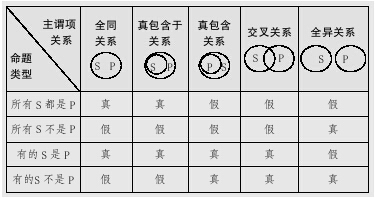
(2)直言命题的对当关系
直言命题的对当关系即不同直言命题之间在真假方面所存在的制约关系。
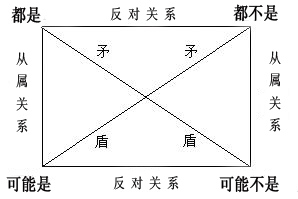
以上图片中的关系可以解释为:
“所有A都是B”与“有的A可能不是B”、“所有A都不是B”与“有的A可能是B”是矛盾关系,它们中必有一真一假。
“所有A都是B”与“所有A都不是B”是上反对关系,它们中必有一假,可以同为假。
“有的A可能是B”与“有的A可能不是B”是下反对关系,它们中必有一真,可以同为真。
“有的A可能是B”包含于“所有A都是B”,可以由“所有A都是B推出”;“有的A可能不是B”包含于“所有A都不是B”,可以由“所有A都不是B”推出。
(3)直言命题的变形推理
直言命题的变形推理就是通过改变前提中直言命题的联项或主项与谓项的位置,从而推出结论的推理。包括换位推理与换质推理。
1、换位推理
换位推理即通常所说的“倒过来说”,就是通过改变前提中直言命题的主项和谓项的位置,从而得出结论的推理方法。
“所有A是B”可以换位为“有些B是A”,如:所有苹果是水果→有些水果是苹果;
“所有A不是B”可以换位为“所有B不是A”,如:所有苹果不是香蕉→所有香蕉不是苹果;
“有些A不是B”可以换位为“有些B是A”,如:有些学生是党员→有些党员是学生;
“有些A不是B”无法进行换位,如:有些学生不是党员不能换位成有些党员不是学生。
2、换质推理
换质推理即通常所说的“换一个说法”,就是通过改变前提中直言命题的联项,从而推出结论的推理方法。
“所有A是B”可以换质为“所有A不是非B”,如:所有文字都是有意义的→所有文字不是没有意义的;
“所有A不是B”可以换质为“所有A是非B”,如:所有人都不是完美的→所有人都是不完美的;
“有的A是B”可以换为“有的A不是非B”,如:有的嫌疑人是有罪的→有的嫌疑人不是没有罪的;
“有的A不是B”可以换为“有的A是非B”,如:有的嫌疑人不是有罪的→有的嫌疑人是没有罪的。
二、三段论推理
三段论推理是由两个直言命题作为前提和一个直言命题作为结论而构成的推理。其中两个前提中包含有三个不同的概念,且在前提和结论中,每个概念都出现两次。例如:所有的糖都是甜的,棒棒糖是糖,所以棒棒糖是甜的。
三段论推理需要遵循一定的规则,常用的有以下两种规则:
(1)一特则特:两个前提不能都是特称命题,且只要前提有一个为特称,则结论为特称。特称命题即为含“有的”的之言命题,如“有的学生是党员”就是一个特称命题。
例如,“有的学生是党员”和“有的学生是大学生”并不能推出任何结论;而“有的动物是鱼”和“所有鱼都生活在水里”,只能推出“有的动物生活在水里”这一特称命题。
(2)一否得否:两个前提不能都是否定命题,且只要前提有一个为否定,则结论为否定。
例如,“所有学生都不是志愿者”和“小李不是学生”并不能推出任何结论;而“所有学生都不是志愿者”和“小李是志愿者”,只能推出“小李不是学生”这一否定命题。
三、复言命题
复言命题是由两个或多个单句通过联结词联结而成的命题。根据逻辑联结词的不同,可以将复言命题划分为联言命题、选言命题和假言命题。
(1)联言命题:联言命题就是将若干个命题联合起来,表示这些情况同时存在的命题。日常联言命题的逻辑联结词还有“是…也是…”、“不仅…还…”、“…同时…”等。
可表示为:p并且q(p、q是联言肢,“并且”是联结词)。
联言命题的推理规则为“一假即假,全真才真”,具体解释为:
1.全部肢命题为真推出联言命题为真;
2.其中有一个肢命题为假,那么联言命题就为假。
例如: “小李是中国人”和“小李是学生”同时为真时才可以推出“小李是中国人且小李是学生”这一命题。
(2)选言命题:选言命题就是给出若干个命题,可以选择出一种或者多种情况存在的命题。根据所能选择的情况不同,可以分为两种:
1. 相容选言命题:多种情况可以同时存在。可表示为:p或者q(p、q是选言肢,“或者”是联结词)。其真假关系为“一真即真,全假才假”。
2. 不相容选言命题:只允许一种情况存在。可表示为:要么p,要么q(p、q是选言肢,“要么……要么……”是联结词)。其真假关系为“同真同假为假,一真一假为真”。
选言命题的推理规则可以通过以下表格来表示:
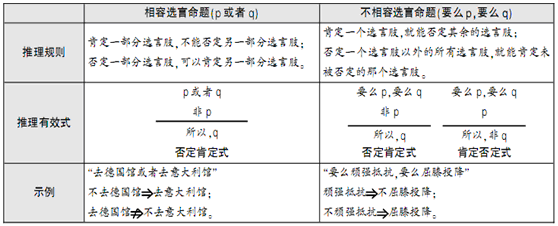
(3)假言命题:假言命题就是带有假设条件的命题。假言命题通常包含两个肢命题:反映条件的肢命题在前,称为前件;反映结果的肢命题在后,称为后件。根据前后件间条件关系的不同,又可分为三种:
1. 充分条件假言命题:当条件p存在时,结论q一定成立,而无需考虑其他条件,则p是q的充分条件,即“有它就行”。可表示为:如果p,那么q或p→q(p是前件,q是后件,“如果……那么……”是联结词)。其推理规则为“肯前肯后,否后否前;肯后不肯前,否前不否后”。
2. 必要条件假言命题:当条件p不存在时,结论q一定不成立,则p是q的必要条件。即“没它不行”。可表示为:只有p,才q或p←q(p是前件,q是后件,“只有……才……”是联结词)。其推理规则为“否前否后,肯后肯前;肯前不肯后,否后不否前”。
3. 充分必要条件假言命题:表示p是q的充分条件和必要条件的命题,即表示p与q等值的命题。可表示为:p当且仅当q(p是前件,q是后件,“当且仅当”是联结词)。其推理规则为“肯前肯后,否前否后;肯后肯前,否后否前”。
四、模态命题
模态命题即含有“必然”、“可能”等模态词的命题。模态命题主要存在两组矛盾,即“必然p”与“可能非p”、“必然非p”与“可能p”。如“今天必然是晴天”与“今天可能不是晴天”是一组矛盾关系,“今天必然不下雨”与“今天可能下雨”是一组矛盾关系。
否定模态命题,即在命题前加否定词,得到其矛盾命题,
并非“必然p”=“可能非p”,即不必然=可能不;
并非“必然非p”=“可能p”,即不必然不=可能;
并非“可能p”=“必然非p”,即不可能=必然不
并非“可能非p”=“必然p”,即不可能不=必然

